6^th International Conference on Theoretical and Applied Physics May 16-17, 2019 Hotel Holiday Inn, Aurelia Rome, Italy

Biography:

Prof. Vasily Yu. Belashov, PhD (Radiophysics), DSci (Physics and Mathematics). Main fields: theory and numerical simulation of the dynamics of multidimensional nonlinear waves, solitons and vortex structures in plasmas and other dispersive media. Presently, he is Chief Scientist and Professor at the Kazan Federal University. He was Coordinator of studies on the International Program “Solar Terminator” (1987-1992), and took part in the International Programs WITS/WAGS and STEP. He is author of 310 publications including 7 monographs. Main books: Solitary Waves in Dispersive Complex Media. Theory, Simulation, Applications. Springer-Verlag GmbH, 2005; Solitons: Theory, Simulation, Applications. Kazan, Kazan Federal University, 2016.

Abstract:

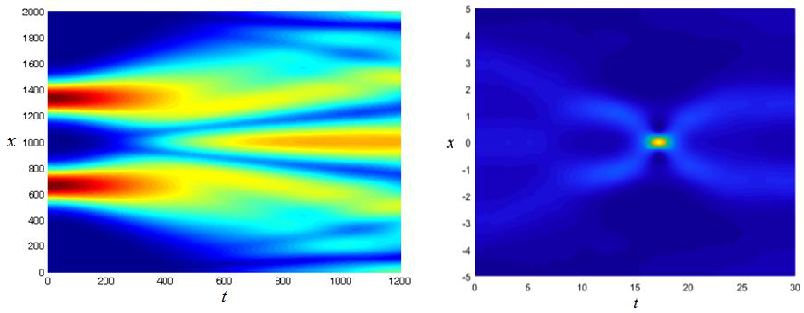
Investigation of dynamics of multidimensional electromagnetic (EM) waves in plasma, such as 2D and 3D envelop solitons, is very actual problem. The interaction sufficiently changes the characteristics of the waves and background EM field in the region of interaction. Problem of the dynamics and stability becomes more complicated if it is necessary to take into account an influence of different dispersive and nonlinear inhomogeneities and nonstationary parameters of medium on the soliton structure and evolution. In this case the problem reduces to the generalized nonlinear schrodinger (GNLS) equation for the amplitude of the EM field with coefficient functions having spatial and temporal inhomogeneities. The analysis of stability of the multidimensional GNLS solitons was based on the method of study of transformational properties of the Hamiltonian of the system developed by authors earlier for the BK class of the equations. As a result we have found the conditions of existence of the multidimensional stable GNLS soliton solutions. At simulation the Fourier splitting method for the GNLS equation was used taking into account the inhomogeneities of coefficient functions of the equation. Implicit scheme of finite-difference method was used for investigation of soliton propagation in non-uniform and nonstationary medium. Numerical modeling showed that inhomogeneity of medium changes the amplitudes of solitons and nonlinear EM waves, their velocities of propagation, their quantity that is caused by their nonelastic interaction in inhomogeneous medium. Nonstationary medium changes a form of impulse and affects its spectral features. Changes of modulation of the parameters of medium make possible variation of character of nonelastic interaction at solitons attraction-repulsion.

Biography:

Abstract:

Investigation of evolution and interaction of solitary waves and pulses (wave packets) is very actual problem in different fields of physics especially when the medium is non-uniform and its properties depend on time. In this case, as a model, we use the generalized non-linear Schrödinger (GNLS) equation, which describes the waves in a plasma, fiber and planar optical waveguides, taking into account the inhomogeneity and non-stationary of a propagation medium. Earlier we have shoved analytically that the GNLS equation can have stable and quasi-stable solutions of the soliton and breather types and also unstable solutions which disperse with time. In this paper we study the evolution and interaction of the envelop solitons numerically. At simulation the Fourier Splitting Method for the GNLS equation was used and the specially developed implicit scheme of finite-difference method was used for investigation of soliton like structures propagation in non-uniform and non-stationary medium. Numerical modeling showed that inhomogeneity of medium changes the parameters of the envelop solitons such as their amplitudes, velocities and their quantity that is caused by their non-elastic interaction in inhomogeneous medium. Non-stationary medium changes a form of pulses and affects their spectral features. Changes of modulation of the parameters of medium make possible variation of character of non-elastic interaction at solitons attraction repulsion. Obtained results can be useful in numerous applications in plasma physics, nonlinear optics and in many other fields of physics.

Biography:

Abstract:

Materials composed of the group IV elements are promising candidates for designing the nano-optoelectronic devices integrated with Si based circuits. Special requirements concerning the electronic properties of the materials (direct band-gap, high mobility of carriers) can be met via the electronic structure engineering. One of methods of modifying the electronic structure is applying the strain [1, 2, 3], e.g. by the choice of unmatched lattices in epitaxial technologies. In this work the DFT based computational methods have been applied to investigate systematically the effect of strains on electronic structure, with the use of ABINIT program. In reference to available technologies the isotropic as well as uniaxial and biaxial strains for crystallographic planes (100), (110) and (111) in diamond like crystals of C, Si, Ge and Sn have been studied. The systems were strained in the range of +/–4%. The following characteristics have been evaluated as functions of the strain: Poison’s ratios, elastic coefficients, band gaps in between chosen band structure points and band offsets. A detailed discussion of observed effects (considering also the orbital composition of bands) such as indirect direct gap transition, opening/closing the gaps, strain induced symmetry breaking effect and band offsets, the effect of lowering the band gap on electron mobility, will be presented.

Biography:

Abstract:

BioMCP aims to study bio sourced phase change materials for the thermal energy storage in buildings and heating networks. Thermal energy storage is one of the key elements to optimize the use of available energy resources (especially renewable ones) and to improve the energy efficiency of buildings. Phase change materials (PCMs) used for the thermal energy storage are an important class of materials which substantially contribute to the efficient use and conservation of waste heat and solar energy. In this framework, our objective is to develop and study new bio sourced phase change materials, able to compete with water as storage material and presenting improved performances in comparison with currently used PCM (ie: low cost, high energy density, low ecological impact). Among bio-based materials, Xylitol has a high potential as a thermal energy material. Its melting point is inferior to 95°C which allows combining the storage unit containing Xylitol with cheap solar collectors. Its latent heat is superior to 263 J.g^-1 and its total energy density is 4-5 times higher than the one of water (110-150 kWh.m^-3 whereas it is approximately 30 kWh.m^-3 for water on a seasonal basis). Its high and stable undercooling allows long-term storage in a metastable state with reduced thermal losses and a negligible risk of spontaneous discharge. However, the activation of the energy discharge process (crystallization activation) is difficult and the subsequent crystallization rates (discharge powers) are very low. Our work in the framework of the FP7 EU SAM.SSA Project, coordinated by Elena Palomo Del Barrio, aims at finding out an easy to implement and efficient solution to discharge the storage unit at the required power when needed. This means being able to trigger nucleation at any time (or temperature) followed by a crystallization of the entire phase change material in due time. Different techniques to crystallize Xylitol have hence been considered. Finally, the feasibility of an innovative, efficient and low intrusive technique to activate the energy discharge is proven. Bubble agitation is a very promising technique. Our work focuses on providing a better understanding of the influence of bubbling on crystallization, on identifying key related variables and on paving the way for bubbling conditions optimization.

Biography:

Abstract:

An anomaly of strong radial magnetic field near the galactic center (GC) is detected. The lower limit of the radial magnetic field at r = 0.12 pc from the GC. Its possible scientific significances are following: The black hole model at the GC is incorrect. The reason is that radiations observed from the region neighbour of the GC are hardly emitted by the gas of accretion disk due to which it is being prevented from approaching to the GC by the abnormally strong radial magnetic field. This is an anticipated signals for existence of magnetic monopoles (MM). The lower limit of the detected radial magnetic field is quantitatively in agreement with the prediction of our paper “An AGN Model with MM”. Magnetic monopoles may play a key role in some very important astrophysical problems using the Robakov Callen effect that nucleons may decay catalyzed by MM. Taking the RC effect as an energy source, we have proposed a unified model for various supernova explosion including to solve the question of the energy source both in the earth core and in the white dwarfs. We may explain the physical reason of the hot big bang of the universe with the similar mechanism of supernova explosion by using the RC effect as an energy source.

Biography:

Abstract: